Shor’s Algorithm: Breaking RSA and ECC Encryption - Part 3

We’ll continue from the previous article on Shor’s algorithm, where we paused at the third goal of applying the inverse quantum Fourier transform (QFT$^{-1}$) to extract the binary representation of the phase:

\[\varphi = 0.\varphi_1\varphi_2\ldots\varphi_t,\]

by transforming this complicated superposition into a simple state of

\[\ket{\varphi_1\varphi_2\ldots\varphi_t}.\]

Goal 3: Transforming the Superposition into Clean State (QFT$^{-1}$)

Goal: Given a superposition of states:

\[\frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}},\]

transform it into the clean state $\ket{\varphi_1\varphi_2\ldots\varphi_t}$.

This goal is achieved by the inverse quantum Fourier transform (QFT$^{-1}$), which reverses the transformation performed by the quantum Fourier transform (QFT). Since the QFT is a unitary operator, its inverse is simply the conjugate transpose. To better understand how to achieve this goal, it helps to examine the forward transformation performed by the QFT, as solving one naturally solves the other:

Goal (inverse): Given the clean state $\ket{\varphi_1\varphi_2\ldots\varphi_t}$, transform it into the superposition of states:

\[\frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}}.\]

Quantum Fourier Transform (QFT)

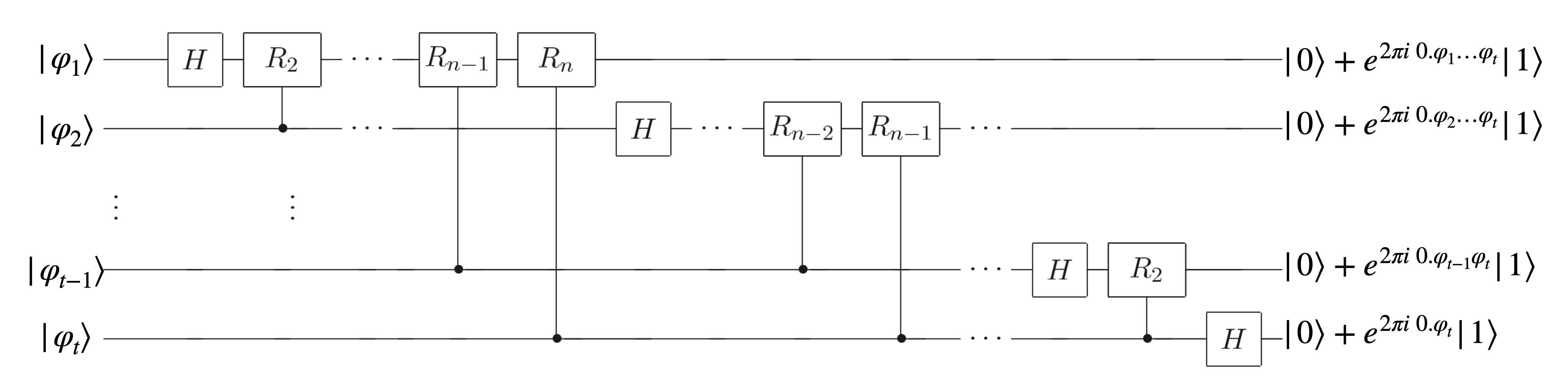
The diagram above illustrates the quantum Fourier transform (QFT) circuit. The clean state $\ket{\varphi_1\varphi_2\ldots\varphi_t}$ is input to the QFT, which transforms it into the superposition of states:

\[\frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}}.\]

The unitary operator $R_k$ is a gate that modifies the phase of the state $\ket{1}$ by $2\pi/2^k$, and defined as:

\[R_k = \begin{pmatrix} 1 & 0 \\ 0 & e^{2\pi i/2^k} \end{pmatrix}, \quad R_k \ket{0} = \ket{0}, \quad R_k \ket{1} = e^{2\pi i/2^k} \ket{1}.\]

Then, the operation of the QFT circuit becomes intuitive. Consider the first qubit of the state $\ket{\varphi_1}$. The Hadamard gate acts on this qubit to create a superposition of $\ket{0}$ and $\ket{1}$, determined by whether $\varphi_1$ is 0 or 1:

\[H\ket{\varphi_1} = \frac{1}{\sqrt{2}}\prths{\ket{0} + (-1)^{\varphi_1}\ket{1}} = \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_1}\ket{1}}.\]

Next, the controlled-$R_2$ gate applies a phase factor $e^{2\pi i\;0.01}$, controlled by the second qubit $\varphi_2$. This is equivalent to applying a phase factor $e^{2\pi i0.0\varphi_2}$ to the $\ket{1}$ component of the first qubit. After this step, the state of the first qubit becomes:

\[\frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2}\ket{1}}.\]

Continuing this process, each subsequent controlled-$R_k$ gate introduces a phase factor determined by the corresponding qubit $\varphi_k$. By the time the process reaches the $t$-th qubit, the state of the first qubit becomes:

\[\frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}},\]

which represents the first qubit of the desired superposition state. Similarly, the second, third, and all subsequent qubits undergo analogous transformations, leading to the desired superposition state shown on the right side of the QFT circuit diagram.

This sequence of operations completes the transformation of the clean input state $\ket{\varphi_1\varphi_2\ldots\varphi_t}$ into the desired superposition of states. Applying the QFT$^{-1}$ then reverses this transformation, recovering the clean state from the superposition, as required.

QED!

I’m afraid we’re out of goals! We’ve successfully broken down the core problems of Shor’s algorithm into manageable sub-goals, and demonstrated how each sub-goal can be achieved.

Complexity Analysis

Space Complexity

The space complexity of Shor’s algorithm is minimal, as the quantum circuit only requires enough qubits to encode the output of the function $f$. Since the size of the output is logarithmic in the problem size $N$ (e.g., for factoring $N$ or solving discrete logarithm problems over a field of size $p$), the space complexity is $O(\log N)$.

Time Complexity

The time complexity depends on the specific encryption scheme being targeted, as the quantum implementation of the function $f$ varies.

1. RSA (IFP): For RSA, the most computationally expensive step is modular exponentiation, which is implemented in the quantum circuit with a time complexity of $O(\log^3 N)$, where $N$ is the number to be factored.

2. ECC (ECDLP): For ECC, according to Martin et al., the complexity depends on the arithmetic operations over the finite field and is estimated to be $O(\log^3 p \log\log p)$, where $p$ is the order of the finite field.