Shor’s Algorithm: Breaking RSA and ECC Encryption - Part 2

We’ll continue from the previous article on Shor’s algorithm, where we paused at the reduction of the integer factorization problem (IFP) and elliptic curve discrete logarithm problem (ECDLP) to the period-finding problem.
Goal 1: Period-Finding Problem
Having reduced the IFP and ECDLP to the period-finding problem, let’s now focus on solving this key problem. For simplicity, we’ll work with univariate functions, though the algorithm generlizes to multivariate cases.
Goal: Given a function $f(x)$, find the smallest integer $r$ such that $f(x) = f(x + r)$.
Function as a Unitary Operator
To leverage quantum computing, we represent the function $f(x)$ as a quantum circuit, which implements a unitary operator $U_f$. The operator acts on a register of qubits encoding the function’s input and outputs:
\[U_f \ket{f(x)} = \ket{f(x+1)}.\]Here, $\ket{f(x)}$ is a quantum state encoding the value of $f(x)$. For example, if $f(x)$ outputs integers from 0 to 7, $\ket{f(x)}$ would be a state of 3 qubits: $\ket{0}$ would be $\ket{000}$, and $\ket{7}$ would be $\ket{111}$.
The challenge is to extract information about the period $r$ from the unitary operator $U_f$. This is where eigenstates and eigenvalues play a crucial role.
Eigenvectors and Eigenvalues
For those unfamiliar with these terms, here’s a quick explanation: in linear algebra, eigenvectors (or eigenstates) are special vectors associated with a matrix. When a matrix $U$ acts on its eigenvector $\ket{\psi}$, the result is simply the eigenvector scaled by a constant factor, called the eigenvalue. Mathematically:
\[U \ket{\psi} = \lambda \ket{\psi},\]where $\ket{\psi}$ is an eigenvector, and $\lambda$ is its corresponding eigenvalue. This relationship makes eigenvectors and eigenvalues crucial in understanding the behavior of matrix operators like $U$.
Eigenstates of $U_f$
The key insight is that the eigenstates and eigenvalues of $U_f$ encode information about the period of the function $f$. By leveraging the periodicity in $f$, we can construct eigenstates related to this periodicity. Even though we don’t know the period $r$, we know it exists. Let’s build an eigenstate $\ket{u_0}$:
\[\ket{u_0} = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \ket{f(k)} = \frac{1}{\sqrt{r}} \prths{\ket{f(0)} + \ket{f(1)} + \ldots + \ket{f(r-1)}}.\]Why is this an eigenstate? To verify, let’s apply $U_f$ to $\ket{u_0}$:
\[\begin{aligned} U_f \ket{u_0} &= \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} U_f \ket{f(k)} \\ &= \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \ket{f(k+1)} \\ &= \frac{1}{\sqrt{r}} \prths{\ket{f(1)} + \ket{f(2)} + \ldots + \ket{f(r)}} \\ &= \frac{1}{\sqrt{r}} \prths{\ket{f(1)} + \ket{f(2)} + \ldots + \ket{f(0)}} \\ &= \ket{u_0}, \end{aligned}\]where the periodicity ensures $\ket{f(r)} = \ket{f(0)}$. This confirms that $\ket{u_0}$ is an eigenstate of $U_f$ with eigenvalue 1.
We can generalize $\ket{u_0}$ to a family of eigenstates $\ket{u_s}$ for $0 \leq s \leq r-1$:
\[\ket{u_s} = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp{\prths{-\frac{2\pi isk}{r}}} \ket{f(k)},\]The eigenvalue for $\ket{u_s}$ can be calculated by applying $U_f$:
\[\begin{aligned} U_f \ket{u_s} &= \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp{\prths{-\frac{2\pi isk}{r}}} \ket{f(k+1)} \\ &= \exp{\prths{\frac{2\pi is}{r}}} \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp{\prths{-\frac{2\pi isk}{r}}} \ket{f(k)} \\ &= \exp{\prths{\frac{2\pi is}{r}}} \ket{u_s}. \end{aligned}\]Thus, $\ket{u_s}$ is an eigenstate of $U_f$ with eigenvalue $\exp{\prths{\frac{2\pi is}{r}}}$. This eigenvalue contains information about the period $r$, specifically the value of $\frac{s}{r}$.
Preparing Eigenstates Without Knowing $r$
To solve the period-finding problem, we need to find the eigenvalue $\exp{\prths{\frac{2\pi is}{r}}}$ associated with the eigenstate $\ket{u_s}$, which encodes $\frac{s}{r}$, the information about the period $r$.
The quantum phase estimation (QPE) algorithm can estimate the eigenvalue $\exp{\prths{\frac{2\pi is}{r}}}$ for a given unitary operator (like $U_f$) and its corresponding eigenstate $\ket{u_s}$. However, there’s a challenge: QPE requires the eigenstate $\ket{u_s}$ as input, but we don’t know the period $r$, so we cannot prepare $\ket{u_s}$ directly.
Fortunately, we can exploit the structure of the eigenstates and superposition to overcome this challenge.
Recall the eigenstates of $U_f$:
\[\ket{u_s} = \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp{\prths{-\frac{2\pi isk}{r}}} \ket{f(k)},\]where $0 \leq s \leq r-1$. Consider a superposition of all eigenstates $\ket{u_s}$ weighted by a complex phase factor $\exp{\prths{\frac{2\pi isk^\prime}{r}}}$ for some $k^\prime$:
\[\frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi isk^\prime}{r}}} \ket{u_s}.\]Expanding $\ket{u_s}$, this becomes:
\[\begin{aligned} \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi isk^\prime}{r}}} \ket{u_s} &= \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi isk^\prime}{r}}} \frac{1}{\sqrt{r}} \sum_{k=0}^{r-1} \exp{\prths{-\frac{2\pi isk}{r}}} \ket{f(k)} \\ &= \frac{1}{r} \sum_{s=0}^{r-1} \sum_{k=0}^{r-1} \exp{\prths{\frac{2\pi is(k^\prime-k)}{r}}} \ket{f(k)} \\ &= \frac{1}{r} \sum_{k=0}^{r-1} \prths{ \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi is(k^\prime-k)}{r}}} } \ket{f(k)}. \end{aligned}\]The inner sum over $s$,
\[\sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi is(k^\prime-k)}{r}}},\]is nonzero only when $k^\prime = k$, due to the properties of complex exponentials (they sum to zero for $k^\prime \neq k$). When $k^\prime = k$, the sum becomes $r$, leading to:
\[\begin{aligned} \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi isk^\prime}{r}}} \ket{u_s} &= \frac{1}{r} \prths{ 0 \ket{f(0)} + 0 \ket{f(1)} + \ldots + r \ket{f(k^\prime)} + \ldots + 0 \ket{f(r-1)} } \\ &= \ket{f(k^\prime)}. \end{aligned}\]If we set $k^\prime$ to $0$, we get:
\[\frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \exp{\prths{\frac{2\pi is \cdot 0}{r}}} \ket{u_s} = \frac{1}{\sqrt{r}} \sum_{s=0}^{r-1} \ket{u_s} = \ket{f(0)}.\]This result shows that the state $\ket{f(0)}$, which we can prepare without knowing the period $r$, is a uniform superposition of all eigenstates $\ket{u_s}$! Therefore, $\ket{f(0)}$ can serve as an input to QPE to estimate the eigenvalues of $U_f$.
Extracting the Period $r$
Applying QPE to $\ket{f(0)}$ produces a random fraction $\frac{s}{r}$ since $\ket{f(0)}$ is a superposition of all $\ket{u_s}$. Repeating QPE multiple times gives a set of fractions $\frac{s_1}{r}$, $\frac{s_2}{r}$, $\ldots$, $\frac{s_n}{r}$, with the common denominator $r$. It is proven that we can efficiently deduce the period $r$ from these fractions.
For example, suppose QPE yields the following fractions:
\[\frac{1}{6}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{5}{6}.\]The common denominator of these fractions is 6, revealing the period $r$ of $f$.
Reduction to Eigenvalue-Finding Problem
By recognizing the fact that $\ket{f(0)}$ is a superposition of all $\ket{u_s}$, we can effectively use the quantum phase estimation (QPE) algorithm—an oracle for finding eigenvalues—to find the eigenvalues of $U_f$, and, consequently, the period $r$.
This reduction shows that solving the period-finding problem reduces to solving the eigenvalue-finding problem via QPE. Through multiple runs of QPE, we can effectively determine the period $r$.
Goal 2: Eigenvalue-Finding Problem (QPE)
Goal: Given a unitary operator $U$ and an eigenstate $\ket{u}$, find $\varphi$ such that $e^{2\pi i\varphi}$ is the eigenvalue of $U$
The quantum phase estimation (QPE) algorithm is a quantum computing algorithm designed to solve this problem. It determines the phase $\varphi$, which encodes information about the eigenvalue $e^{2\pi i\varphi}$ of a unitary operator $U$, acting on an eigenstate $\ket{u}$.
QPE Algorithm: First Half
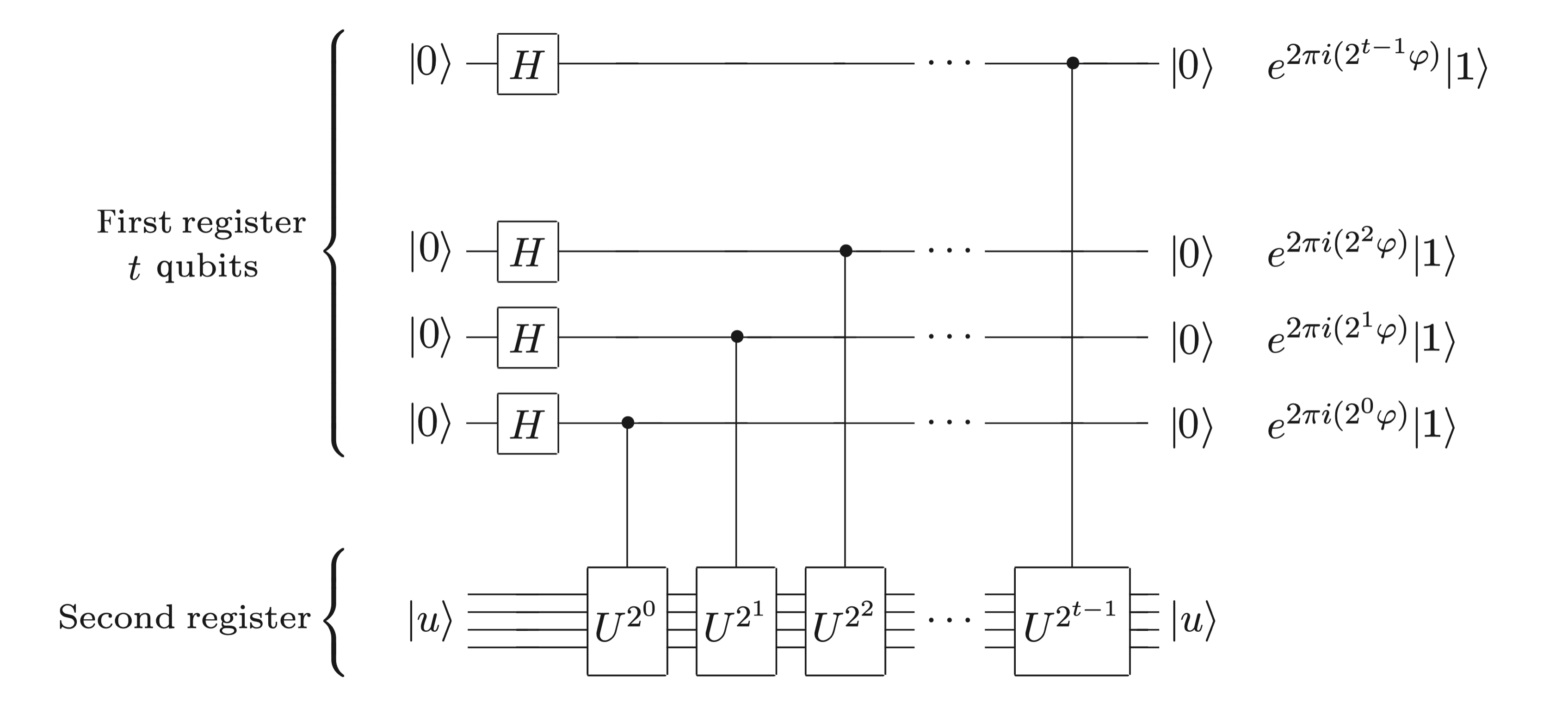
The diagram above illustrates the first half of the QPE algorithm. It uses two qubit registers:
- First Register: Contains $t$ qubits initialized to $\ket{0}$.
- Second Register: Prepared in the eigenstate $\ket{u}$.
The algorithm proceeds as follows:
-
Apply a Hadamard gate to each qubit in the first register. This creates a uniform superposition.
-
Apply controlled-$U^{2^0}$ gate to the second register, controlled by the first qubit (the bottom-most qubit) of the first register.
The operator $U^{2^0}$ applies unitary operator $U$ $2^0$ times. This operator is controlled by the first qubit of the first register:
- If the control qubit is in state $\ket{1}$, $U^{2^0}$ is applied to the second register.
- If the control qubit is in state $\ket{0}$, $U^{2^0}$ is not applied.
Since the control qubit is in superposition, $U$ is applied to only the part of the second register that corresponds to the $\ket{1}$ component of the first register’s superposition.
Given that $\ket{u}$ is an eigenstate of $U$, the application of $U^{2^0}$ leaves $\ket{u}$ unchanged, but introduces a phase factor $e^{2\pi i (2^0 \varphi)}$ (the eigenvalue of $U$) to the $\ket{1}$ component of the control qubit.
-
Sequentially apply controlled-$U^{2^j}$ gate to the second register, controlled by the $j$-th qubit of the first register, for $j = 0, 1, \ldots, t-1$ (we’ve already applied the $j=0$ case in the previous step).
Each controlled-$U^{2^j}$ applies $U$ $2^j$ times, when the corresponding control qubit is in state $\ket{1}$.
For each controlled operation, the phase factor $e^{2\pi i(2^j \varphi)}$ is introduced to the $\ket{1}$ part of the control qubit, encoding the eigenvalue’s phase information in the first register.
Now the first register is in a superposition of states, each encoding a phase factor related to $\varphi$:
\[\frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^0 \varphi)}\ket{1}} \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^1 \varphi)}\ket{1}} \otimes \ldots \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^{t-1} \varphi)}\ket{1}}\]To simplify, let’s represent the phase factor $\varphi$, the yet-to-be-determined phase factor, as a binary fraction:
\[\varphi = 0.\varphi_1\varphi_2\ldots\varphi_t,\]where $\varphi_j$ represents the $j$-th bit of $\varphi$. The integer part of $\varphi$ can be ignored, as it does not contribute to the phase $e^{2\pi i\varphi}$. Now the phase factors can be expressed using the binary fraction (observe the placement of the dot):
\[e^{2\pi i(2^j \varphi)} = e^{2\pi i(2^j \cdot 0.\varphi_1\varphi_2\ldots\varphi_t)} = e^{2\pi i(\varphi_1\ldots\varphi_j.\varphi_{j+1}\ldots\varphi_t)} = e^{2\pi i(0.\varphi_{j+1}\ldots\varphi_t)}.\]Substituting this into the state of the first register, the superposition becomes:
\[\begin{aligned} & \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^0 \varphi)}\ket{1}} \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^1 \varphi)}\ket{1}} \otimes \ldots \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i(2^{t-1} \varphi)}\ket{1}} \\ = & \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \frac{1}{\sqrt{2}}\prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}} \\ = & \frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}}. \end{aligned}\]QPE Algorithm: Second Half
After the first half of the QPE algorithm, the first register is in the state:
\[\frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}}.\]The goal is to extract the binary representation of the phase:
\[\varphi = 0.\varphi_1\varphi_2\ldots\varphi_t,\]by transforming this complicated superposition into a simple state of
\[\ket{\varphi_1\varphi_2\ldots\varphi_t}\]so that we can measure the first register to obtain the binary fraction $\varphi$.
Fortunately, this transformation is achieved by the inverse quantum Fourier transform (QFT$^{-1}$), which effectively “decodes” the phase information encoded in the relative phases of the superposition.
By assuming we have the QFT$^{-1}$ as an oracle, the eigenvalue-finding problem is solved! The process concludes with measuring the first register to directly obtain the binary fraction $\varphi$.
This reduces the eigenvalue-finding problem to the problem of transforming the quantum state:
\[\frac{1}{\sqrt{2^t}}\prths{\ket{0} + e^{2\pi i0.\varphi_1\varphi_2\ldots\varphi_t}\ket{1}} \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_2\ldots\varphi_t}\ket{1}} \otimes \ldots \otimes \prths{\ket{0} + e^{2\pi i0.\varphi_t}\ket{1}}.\]into the clean state:
\[\ket{\varphi_1\varphi_2\ldots\varphi_t}.\]We’ll explore the third goal of applying the QFT$^{-1}$ to achieve this transformation in the next article.
All images were drawn by the author—except the first, generated by ChatGPT.

Leave a comment