Superconducting Qubits

Introduction

Superconductors are special kind of material that, when cooled down to extremely low temperatures, can conduct electricity with zero resistance. That means electric current can flow through them forever without losing energy as heat.

Even more interestingly, superconductors also expel magnetic fields (a property called Meissner effect) and allow for the creation of unique quantum devices—like the Josephson junction, which is the key building block of superconducting qubits.

In this article, we won’t dive into solving Schrödinger’s equation or calculating eigenstates (though if you’re into that, you might consider majoring in physics—or just checking out one of the many great resources online).

LC Circuit and Standing Waves

Superconductors behave like perfect electric wires, which can be used to create classical electrical circuits (not to be confused with quantum circuits used in algorithms). In particular, we’re interested in LC circuits, made from an inductor (L) and a capacitor (C) connected in a loop:

Image source

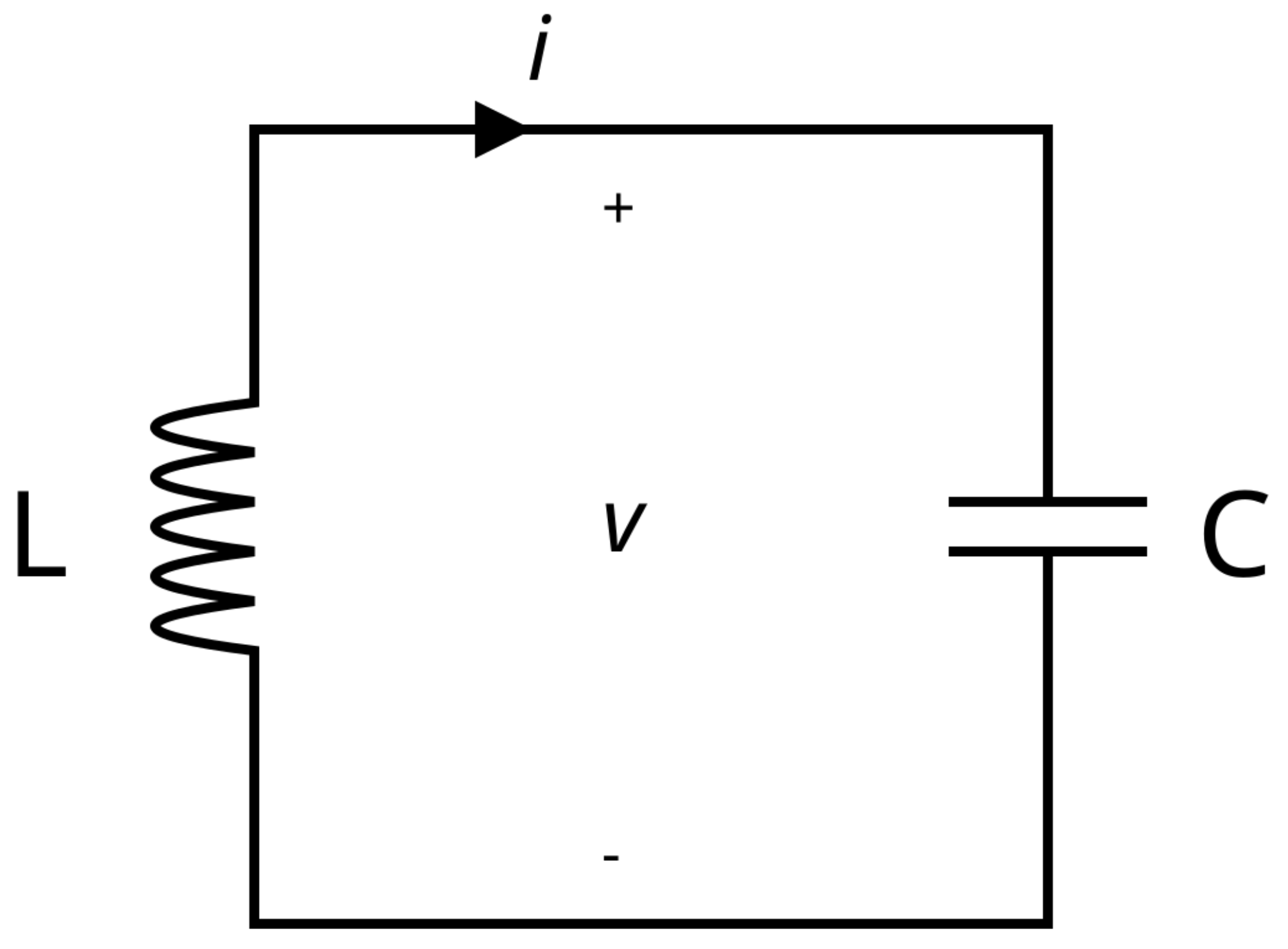
You can think of an LC circuit like a guitar string.

• The inductor (L) stores energy in the form of current flow (which creates magnetic field), similar to how the motion of a vibrating string carries kinetic energy.
• The capacitor (C) stores energy in the form of electric charge, like a stretched string holds energy in its tension.

As the guitar string vibrates—trading energy between tension and motion—the LC circuit oscillates between current and charge.

Now here’s the key: just like a guitar string only vibrates at certain frequencies (called harmonics), the LC circuit also has discrete energy levels. These are like the “standing waves” in the string, and they arise from interference of oscillations traveling in opposite directions.

Image source

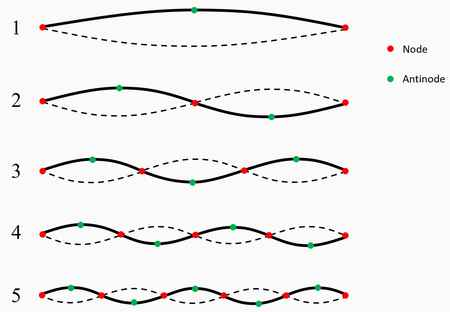
The energy levels in a quantum LC circuit are evenly spaced—just like the harmonic overtones of a string. (Technically, this result comes from solving the Hamiltonian of a quantum harmonic oscillator—which we don’t do here. But if you’re curious, check out this link.)

The Problem

At first glance, it might seem like we can use the first two energy levels as our qubit states $\ket{0}$ and $\ket{1}$. But there’s a problem: the levels are evenly spaced.

If we apply a pulse of energy to drive the $\ket{0} \to \ket{1}$ transition, that same energy could also drive $\ket{1} \to \ket{2}$ or $\ket{2} \to \ket{3}$, and so on. There’s no clean way to isolate just two levels. This makes it impossible to treat the system as a qubit without unwanted leakage into higher states.

Josephson Junction: Adding Non-linearity

Image source

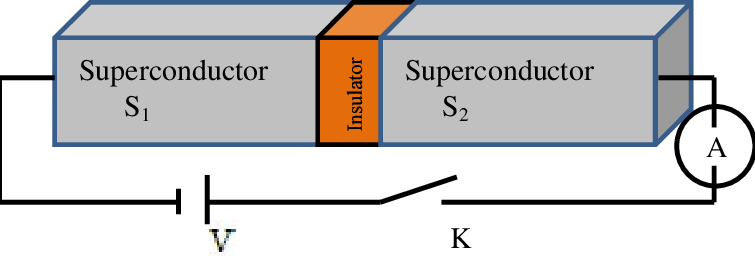
The solution? Add nonlinearity.

That’s what the Josephson junction does. It’s made by sandwiching a thin insulator between two superconductors. This structure creates a nonlinear inductive element that changes the potential energy landscape from a simple parabola (something smooth and perfect) to a cosine-shaped curve (something slightly messy—just enough to break the symmetry).

Going back to our guitar string analogy: adding a Josephson junction is like placing a bit of dirt or tape on the string. The string still vibrates, but its harmonics shift slightly. Now the energy levels are not evenly spaced, which means we can safely isolate and control just $\ket{0}$ and $\ket{1}$.

This nonlinear oscillator is the foundation of superconducting quantum computing.

Manipulating Superconducting Qubits

Now that we’ve isolated a two-level system, we need to manipulate it—i.e., apply quantum gates.

Remember, the Hamiltonian governs how a quantum system evolves over time. So if we temporarily change the Hamiltonian, we can drive the system from one state to another.

This is done using microwave pulses. When applied at the right frequency, the qubit undergoes a Rabi oscillation—a smooth transition between $\ket{0}$ and $\ket{1}$.

To apply a gate, we don’t let the system oscillate forever—we pulse the microwave for a precise amount of time:

• A half-cycle ($\pi$ radians) pulse flips the qubit from $\ket{0}$ to $\ket{1}$: $X$ gate.
• A quarter-cycle ($\pi/2$ radians) pulse rotates the qubit to a superposition of $\ket{0}$ and $\ket{1}$.

The shape, frequency, and duration of the pulse determine exactly what quantum operation is applied.

Measuring Superconducting Qubits

Superconducting qubits are like silent guitar strings—you can’t directly hear (or measure) them. So we couple them to a readout resonator—which acts like an additional string that we can listen to.

Depending on whether the qubit is in $\ket{0}$ or $\ket{1}$, the qubit slightly shifts the resonator’s frequency. By sending a microwave probe into the resonator and measuring the response (phase or amplitude), we can infer the state of the qubit—without directly disturbing it. This is called dispersive readout.

Superconducting Qubit: Pros, Cons and Current Status

Pros

• Fast gates: Gate times are in the tens of nanoseconds.
• Mature technology: Many years of research and development.
• Strong industry support: Backed by IBM, Google, Rigetti, and others.
• Great tools: Powerful software libraries like Qiskit and Cirq.

Cons

• Short coherence times: Qubits lose their state after a few microseconds.
• Cryogenic cooling: Requires operation at $< 15\text{ mK}$ (millikelvin), requiring complex refrigerators.
• Scalability limits: As systems grow, calibration and crosstalk become more challenging.

Current Status

Superconducting qubits are still the most mature and widely developed quantum hardware. IBM has announced its “Kookaburra” processor with over 4,000 qubits. Google, Rigetti, and others continue to advance coherence times, gate fidelities, and qubit interconnects.

Although future platforms like topological qubits may surpass it in fault tolerance, superconducting are currently leading the race toward practical quantum computing.

They’ve come a long way—4,000 qubits is a big milestone. But it’s still not useful. We’re not even close to solving real-world problems. There’s no fault tolerance, no large-scale logical qubits, and circuit depth is still limited by noise and crosstalk.

You might start to wonder: do they believe in the long-term viability of superconducting qubits? Maybe not. What they are clearly focused on is selling cloud-based access to students, universities, and quantum program developers. And to be fair, that’s a good business model. But it’s a business model for education and developer engagement, not for breakthrough quantum computing.

In my opinion, it probably won’t be the one that breaks Ethereum.

All images in this article were generated by ChatGPT, except those explicitly marked with a source link.