Qubits and Entanglement

Cats vs. Qubits

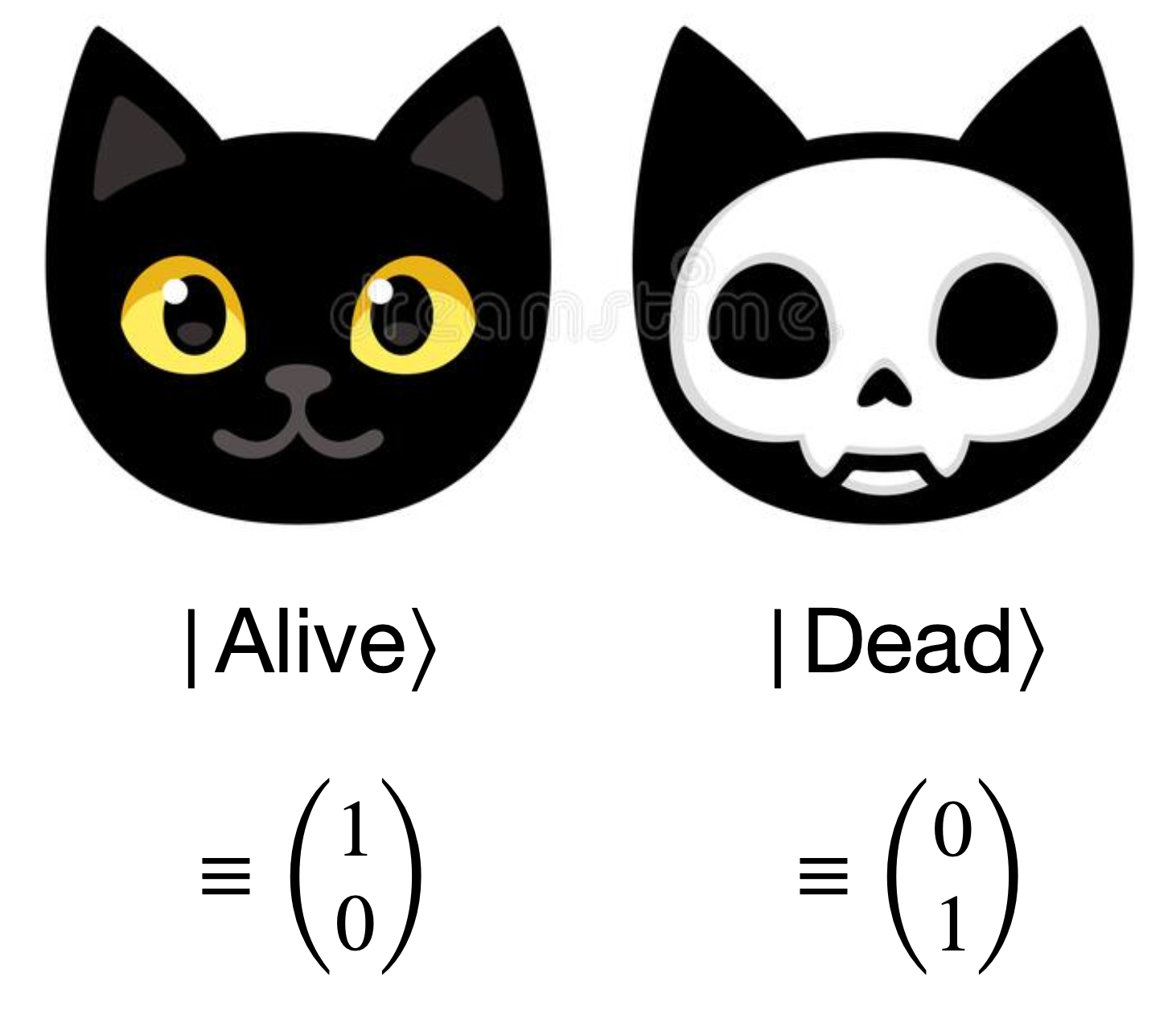
In the last article, we explored quantum states and operators through the example of quantum cats—cats that can exist in states of being alive, dead, or even both at the same time. Now, let’s shift our focus to qubits, the “cats” of quantum computing.

Let’s start by recalling the quantum cat example. In the classical world, a cat can be either alive or dead. These two states are mutually exclusive, meaning the cat cannot be in both states at once. However, in the quantum world, the cat’s quantum state exists in a Hilbert space spanned by two orthogonal basis states: $\ket{\text{alive}}$ and $\ket{\text{dead}}$. These states can be represented in vector form as $\begin{bmatrix} 1 \ 0 \end{bmatrix}$ and $\begin{bmatrix} 0 \ 1 \end{bmatrix}$ (or vice versa). The cat can exist in a superposition of these two states, meaning its quantum state can be represented as a linear combination of these basis states.

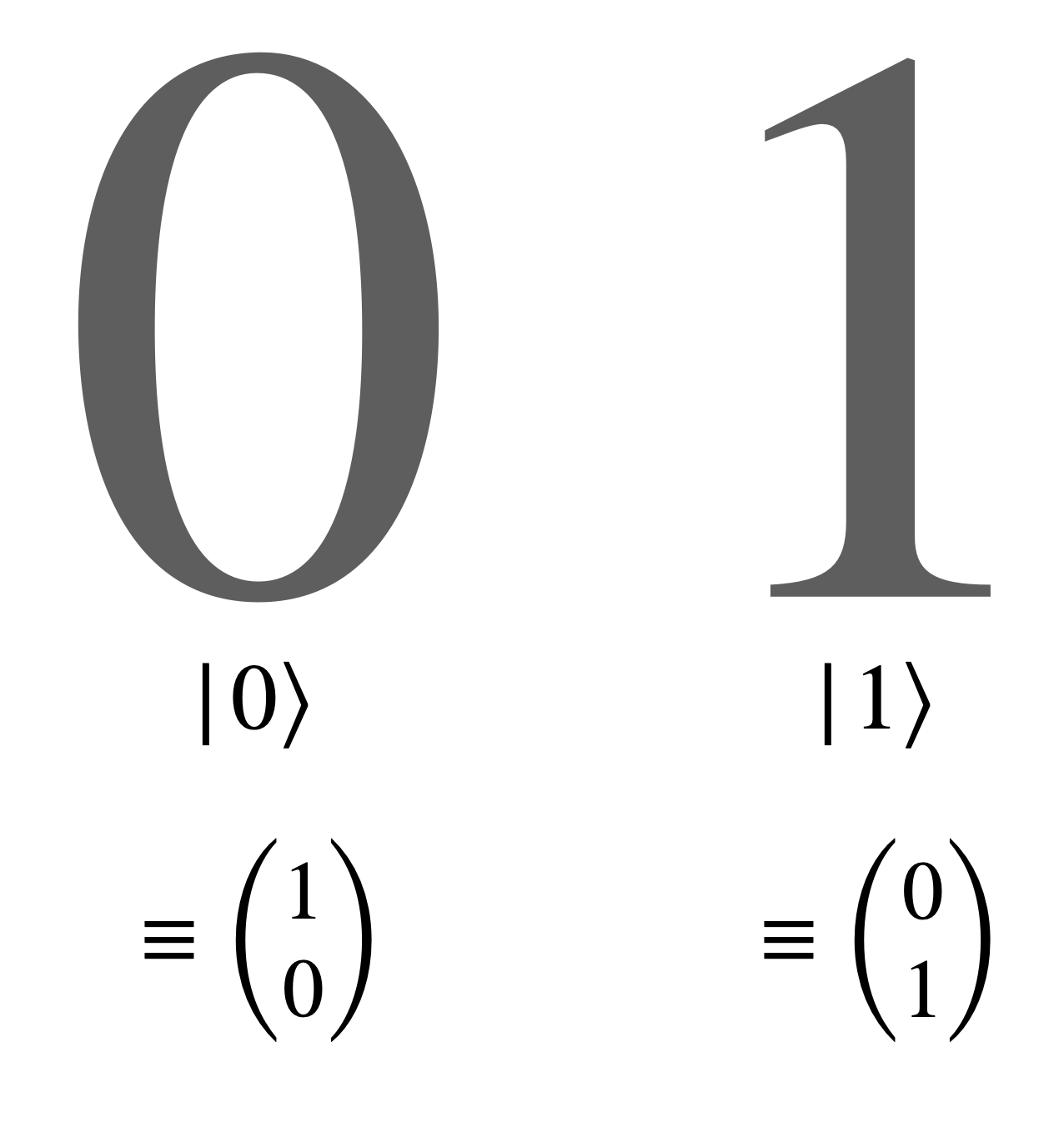
Now, let’s draw the parallel to qubits. The relationship between classical bits in computer science and quantum bits (qubits) mirrors the relationship between classical cats and quantum cats. In the classical world, a bit can be either $0$ or $1$, with these two states being mutually exclusive. In the quantum world, however, a qubit can exist in a superposition of the two states. This means the quantum state of a qubit can be expressed as a linear combination of the two basis states, which we can denote as $\ket{0}$ and $\ket{1}$.

Simply put, a qubit is just like a cat—it can be in a combination of two states at once. While the term “qubit” may sound intimidating, it’s really just a fancy way of describing the bit version of a “quantum cat”. The states $\ket{0}$ and $\ket{1}$ directly correspond to the $\ket{\text{alive}}$ and $\ket{\text{dead}}$ states of the cat, one-to-one.

Multi-Qubit Systems

Just as we can have multiple classical bits in a computer, we can also have multiple qubits in a quantum computer. When dealing with multiple qubits, the quantum state of the system is described using a tensor product (denoted by $\otimes$)of the individual qubit states. You can think of the tensor product as a way of forming a “tuple” of qubits in a physical-mathematical sense. For example, for a two-qubit system, if the first qubit is in state $\ket{0}$ and the second qubit is in state $\ket{1}$, the combined quantum state of the system is:

\[\ket{0} \otimes \ket{1}, \quad \text{or simply,} \quad \ket{01}.\]

This is quite intuitive and mirrors the way we think about combining classical bits.

Basis States of Two-Qubit System

The orthogonal basis states are formed by taking the tensor products of the basis states of each qubit. These basis states are:

\[\ket{00}, \ket{01}, \ket{10}, \ket{11}\]

These states represent all possible configurations of the two qubits, much like how $00$, $01$, $10$, and $11$ represent all possible configurations of two classical bits.

Why is it Called a Tensor “Product”?

The tensor product behaves like a product—it distributes over addition and is associative. For example, consider two identical superposed qubits, each in the state $\frac{1}{\sqrt{2}}(\ket{0} + \ket{1})$. The combined state of the two-qubit system is:

\[\begin{align} \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) &= \frac{1}{2}(\ket{0} \otimes \ket{0} + \ket{0} \otimes \ket{1} + \ket{1} \otimes \ket{0} + \ket{1} \otimes \ket{1}) \\ &= \frac{1}{2}(\ket{00} + \ket{01} + \ket{10} + \ket{11}) \end{align}\]

This shows how the tensor product expands and combines the individual states to form the overall quantum state of the system. Intuitively, the resulting state is a uniform superposition of all possible configurations of the two qubits.

Order Matters: Non-Commutativity of Tensor Product

One important property of the tensor product is that it is not commutative. For instance:

\[\ket{01} \neq \ket{10}\]

This means the order of the qubit matters. A system where the first qubit is in state $\ket{0}$ and the second is in state $\ket{1}$ is different from a system where the first qubit is in state $\ket{1}$ and the second is in state $\ket{0}$. Intuitively, the position of each qubit in the system defines its role and state, making the order significant.

Product States and Entangled States

In a multi-qubit system, quantum states can be classified as either product states or entangled states, depending on whether the state can be expressed as a tensor product of individual qubit states.

Product States

A product state is a quantum state of a multi-qubit system that can be factored into the tensor product of the states of individual qubits. For example, the state:

\[\frac{1}{2}\prths{\ket{00} + \ket{01} + \ket{10} + \ket{11}}\]

is a product state because it can be rewritten as:

\[\frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\]

This factorization implies that the first and second qubits are independent of each other, meaning their states can be described separately.

In a product state, measuring one qubit does not affect the state of the other qubit. For instance, if we measure the first qubit in the state:

\[\frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}),\]

and find it in state $\ket{0}$, the second qubit remains in its original superposition of $\ket{0}$ and $\ket{1}$:

\[\frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \Longrightarrow \ket{0} \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\]

This independence is a defining characteristic of product states.

Entangled States

An entangled state is a quantum state of a multi-qubit system that cannot be expressed as a tensor product of the individual qubit states. The qubits in an entangled state are intrinsically linked, meaning the state of one qubit is dependent on the state of the other.

For example, the state:

\[\frac{1}{\sqrt{2}}(\ket{00} + \ket{11})\]

is an entangled state because it cannot be factored into the tensor product of two single-qubit states.

In an entangled state, measuring one qubit instantly determines the state of the other qubit. For example, if we measure the first qubit in the entangled state:

\[\frac{1}{\sqrt{2}}(\ket{00} + \ket{11})\]

and find it in state $\ket{0}$, the state of the second qubit is immediately determined to be $\ket{0}$:

\[\frac{1}{\sqrt{2}}(\ket{00} + \ket{11}) \Longrightarrow \ket{0} \otimes \ket{0}\]

This “entanglement” between qubits, regardless of their physical separation, is one of the most fascinating and non-intuitive aspects of quantum mechanics—imagine you read a memory block in one computer and instantly, without any delay, the entangled memory block in the other computer located on opposite sides of the planet changes to match.