Building Logical Qubits from Physical Qubits: Quantum Error Correction

Introduction
In the previous article, we explored the no-cloning theorem, which states that we can’t create an exact copy of an arbitrary quantum state. This restriction poses a major challenge for quantum error correction—in classical computing, we protect information by making redundant copies, but in quantum computing, we can’t directly copy qubits.
So if we can’t simply copy qubits, how do we protect quantum information from errors?
The key idea is to spread information across multiple qubits, distributing quantum states in a way that allows us to detect and correct errors without directly measuring the qubits themselves (which would collapse their quantum state).
However, quantum error correction is much more challenging than classical error correction, not only because we can’t copy qubits:
- More types of errors: qubits can also suffer from phase flips, which affect quantum superposition without changing measurement outcomes.
- No direct error detection: detection by measuring a qubit collapses its quantum state, destroying the information we want to protect.
- Errors accumulate over time: Due to decoherence, a quantum system will gradually lose its quantum state, unless continuously corrected.
Despite these challenges, quantum error correction is still possible. In this article, we’ll explore the three-qubit bit flip code, three-qubit phase flip code, and Shor’s 9-qubit code, which provide a foundation for more advanced quantum error correction schemes.
Let’s start by understanding the different types of errors that can affect qubits.
Error Models
Classical error correction primarily deals with bit flips (0 $\leftrightarrow$ 1). In quantum computing, we have additional types of errors:
- Bit flip errors: $\ket{0} \Leftrightarrow \ket{1}$ (like classical bit flips)
- Phase flip errors: $\ket{+} \Leftrightarrow \ket{-}$, where $\ket{+}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$ and $\ket{-}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$
- Bit-phase flip error: Both a bit-flip and a phase-flip occur simultaneously.
To correct these errors, we need quantum error correction codes.
Three Qubit Bit Flip Code
The three qubit bit flip code can correct one bit flip error.
Encoding the Qubit
Given an arbitrary qubit:
\[\ket{\psi} = \alpha \ket{0} + \beta \ket{1},\]we encode it using redundancy:
\[\ket{\psi_0} = \alpha \ket{000} + \beta \ket{111}.\]This encoding is performed by the following circuit:
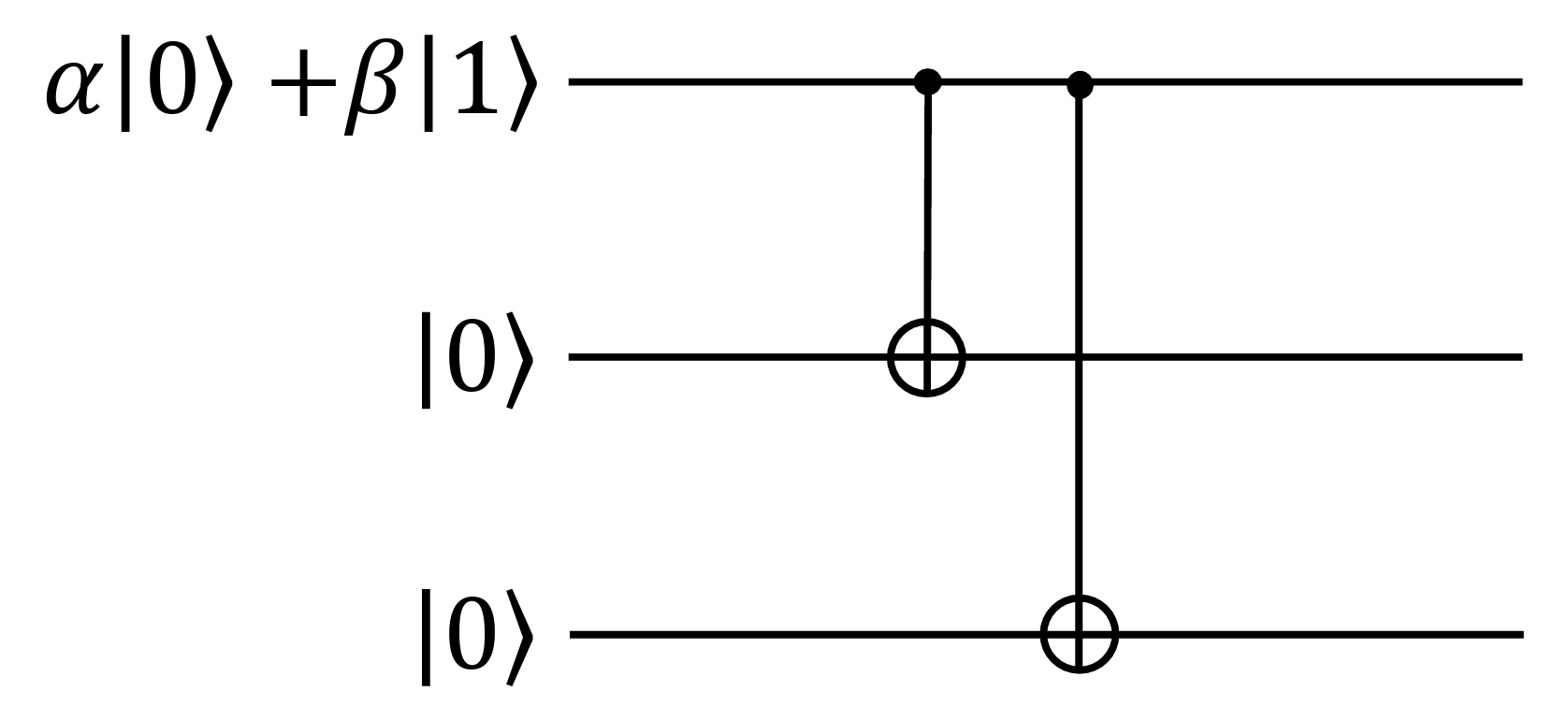
This circuit ensures that:
- $\ket{0}$ (when $\alpha=1$) is encoded as $\ket{000}$
- $\ket{1}$ (when $\beta=1$) is encoded as $\ket{111}$
Since quantum operations are linear, this works for any superposition of $\ket{0}$ and $\ket{1}$.
Error Detection and Correction
If a bit flip occurs on the first qubits in the noisy channel, $\ket{\psi_0}$ becomes:
\[\ket{\psi_0} = \alpha \ket{000} + \beta \ket{111} \Rightarrow \ket{\psi_1} = \alpha \ket{100} + \beta \ket{011}.\]We must detect and correct the error. However, directly measuring the qubits would collapse the quantum state. Instead, we use parity checks (XOR operations):
- Compute parity of first two qubits
- If the parity is 1, one of the first two qubits is flipped
- If the parity is 0, the first two qubits are correct
- Compute parity of last two qubits
- If the parity is 1, one of the last two qubits is flipped
- If the parity is 0, the last two qubits are correct
By comparing these parity results, we can determine which specific qubit is flipped or if no qubit is flipped.
For example, in our case ($\ket{\psi_1} = \alpha \ket{100} + \beta \ket{011}$),
- The parity of the first two qubits is 1: the first or second qubit is flipped
- The parity of the last two qubits is 0: the second and third qubits are correct
Therefore, we can conclude that the first qubit is flipped.
To perform error correction, we use the following quantum circuit, which detects errors without violating the no-cloning theorem:
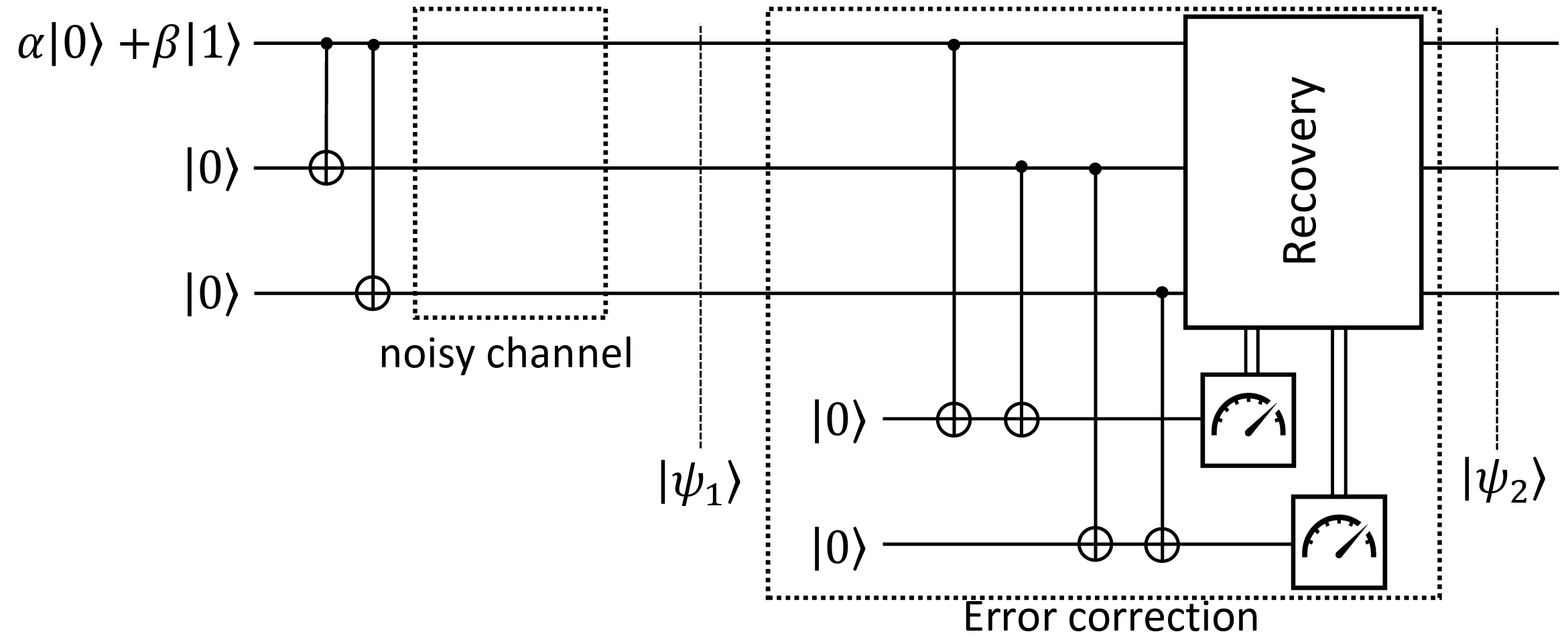
How the circuit works (after the noisy channel):
- Four CNOT gates:
- The CNOT gate is applied controlled by the first two qubits and the last two qubits, saving the parity check results in the additional two qubits, respectively. These CNOT operations acts as XOR operations.
- Measurement of the additional two qubits:
- This gives us information about which qubit has flipped, but not its actual state, preserving the quantum superposition.
- Error correction step:
- Based on the measurement results, we apply $X$ gate (bit-flip) to restore the original state:
The three-qubit bit flip code is a simple but fundamental example of quantum error correction. However, it only corrects bit-flip errors—we need more codes to handle phase-flip and bit-phase-flip errors. We’ll explore phase-flip error correction and how to combine both techniques to create more powerful error correction codes.
Three Qubit Phase Flip Code
The three qubit phase flip code is similar to the three-qubit bit flip code, but instead of correcting bit flips, it corrects phase flips errors.
Encoding the Qubit
Given an arbitrary qubit:
\[\ket{\psi} = \alpha \ket{0} + \beta \ket{1},\]we encode it using a redundancy in a different basis (the $\ket{+}$ and $\ket{-}$):
\[\ket{\phi_0} = \alpha \kettt{+++} + \beta \ket{\texttt{-}\texttt{-}\texttt{-}},\]where $\kettt{+++}$ and $\ket{\texttt{-}\texttt{-}\texttt{-}}$ are:
\[\begin{align*} \kettt{+++} &= \ket{+} \otimes \ket{+} \otimes \ket{+} = \prths{\frac{1}{\sqrt{2}}\prths{\ket{0}+\ket{1}}}^{\otimes 3} \\ \kettt{---} &= \ket{-} \otimes \ket{-} \otimes \ket{-} = \prths{\frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}}}^{\otimes 3} \end{align*}\]This encoding is implemented using the following circuit:
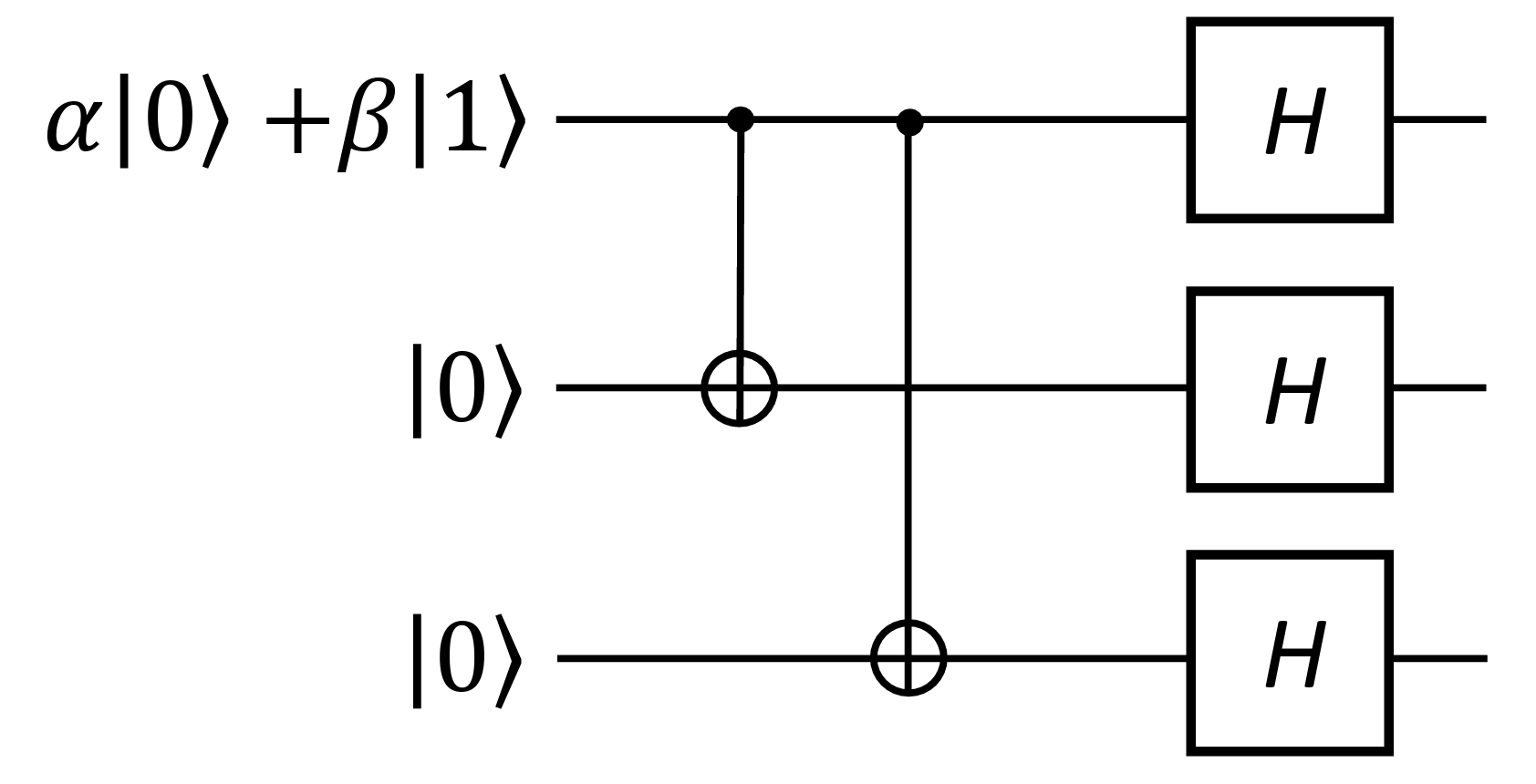
Here’s what happens:
- The first two CNOT gates creates redundancy in the computational basis, similar to the bit flip code.
- The final Hadamard gates converts the state into the $\ket{+}$ and $\ket{-}$ basis (Hadamard basis).
Now, if no errors occur, the state remains in the encoded form:
\[\ket{\phi_0} = \alpha \kettt{+++} + \beta \kettt{---}.\]Error Detection and Correction
If a phase-flip error occurs on first qubit in a noisy channel, the relative phase (sign) between the computational basis states changes:
\[\ket{\psi_0} = \alpha \kettt{+++} + \beta \kettt{---} \Rightarrow \ket{\psi_1} = \alpha \kettt{-++} + \beta \kettt{+--}\]This means that the first qubit flipped from $\ket{+}$ to $\ket{-}$, and vice versa, while the other two qubits remain unchanged.
To detect error, we use parity checks—but this time in the Hadamard basis. Unlike bit-flip errors, phase errors are not directly visible in the computational basis. We first need to convert the state back to the computational basis ($\braces{\ket{0},\ket{1}}$)
- Apply Hadamard gates to all three qubits
- This transforms $\ket{+} \Rightarrow \ket{0}$ and $\ket{-} \Rightarrow \ket{1}$.
- Perform parity checks (XOR operations) on the transformed qubits:
- Similar to the bit flip code, we check the parity of the qubits to detect the error.
The error correction process follows a structure similar to the bit-flip code, using a detection circuit:
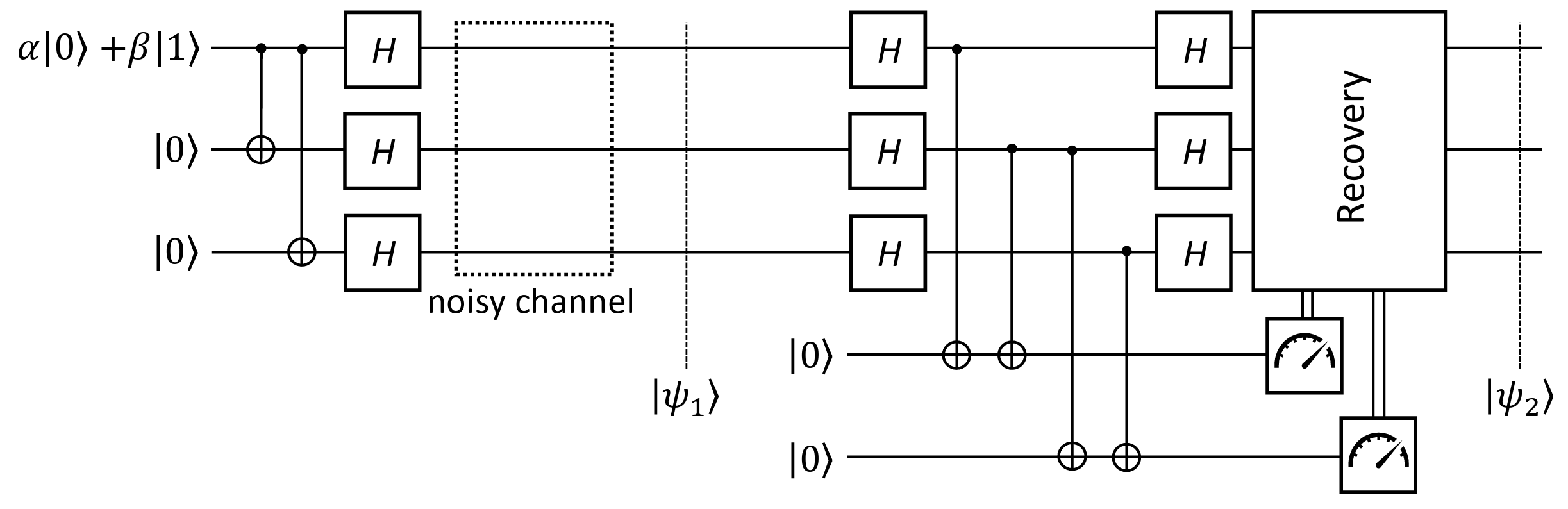
The circuit works similarly to the bit flip code, but with Hadamard gates applied before and after parity checks. The Hadamard gates convert the Hadamard basis states to the computational basis for parity checks, and then back to the Hadamard basis for error correction.
After applying the parity check, we apply the $Z$ (phase flip) gate to the first qubit for recovery:
\[\ket{\psi_1} = \alpha \kettt{-++} + \beta \kettt{+--} \Rightarrow \ket{\psi_2} = \alpha \kettt{+++} + \beta \kettt{---} = \ket{\psi_0}.\]Shor’s 9-Qubit Code
The Shor’s 9-qubit code, introduced by Peter Shor (yes, the same Shor who gave us the famous algorithm), combines both the bit flip and phase flip codes into a single, more powerful scheme. It works by:
- Encoding the qubit using the three-qubit phase flip code.
- Further encoding each of those three qubits using the three-qubit bit flip code.
This redundancy protects against arbitrary single-qubit errors, including bit-flip, phase-flip, and bit-phase-flip errors. The following circuit shows the encoding and error correction process:
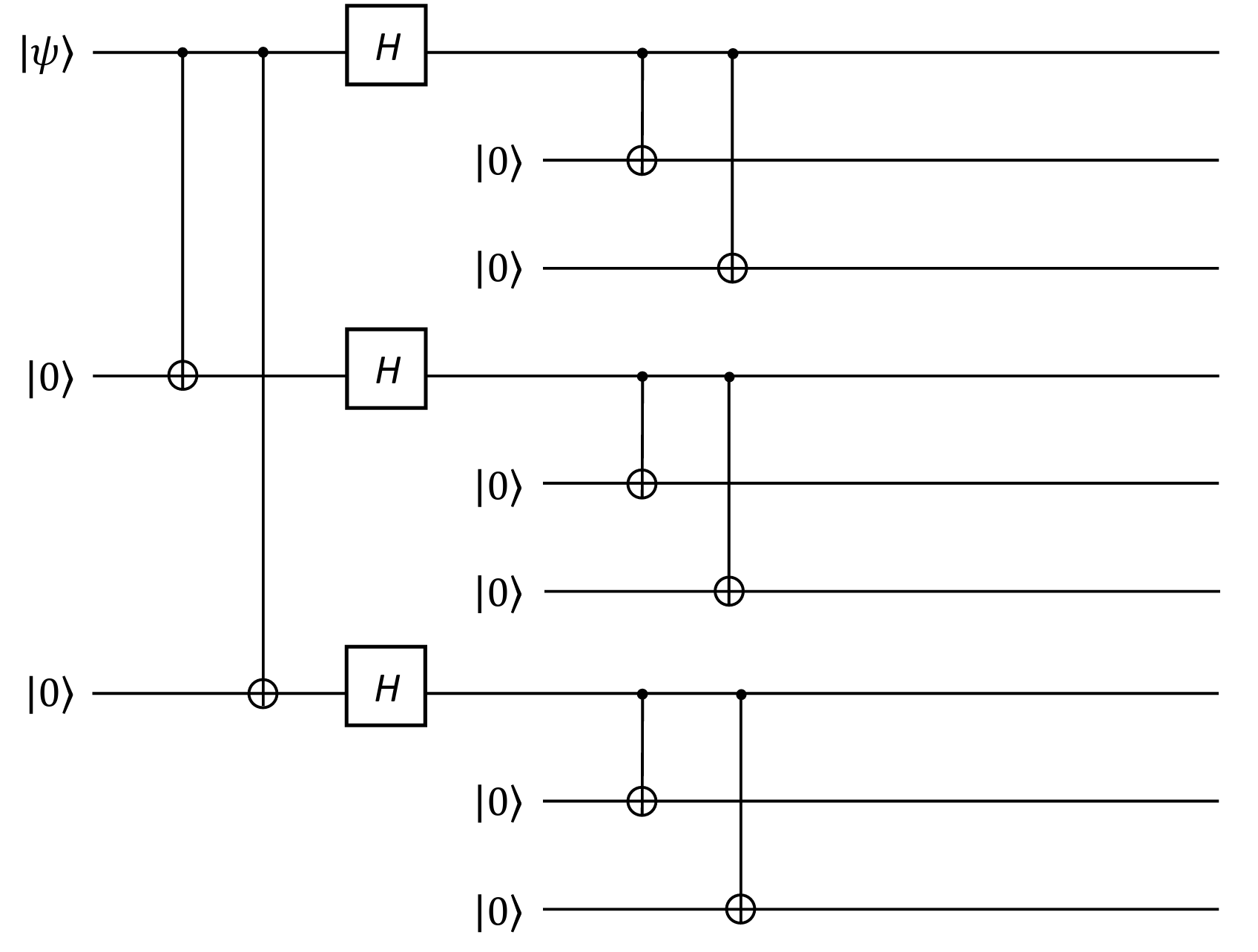
Since the code uses $3\times 3 = 9$ qubits, it is more resource-intensive but offers stronger protection than either the bit-flip or phase-flip codes alone.
Is 9 Qubits Enough?
At this point, you might wonder: Is Shor’s 9-qubit code sufficient to create a fully reliable logical qubit? The answer is no. While it was a significant step forward in quantum error correction, it has fundamental limitations that prevent it from being achieving fault tolerance (qubit reliability over long computations) in real quantum computers.
It Only Corrects Single-Qubit Errors
Shor’s code protects a single logical quit using 9 physical qubits, but it is only designed to correct a single erroneous qubit per encoded block. If two or more physical qubits experience errors at the same time, the scheme can’t correct them.
Unfortunately, as quantum circuits grow more complex, multiple qubits can experience errors at the same time due to:
- Correlated errors: multiple qubits can interact with their environment in the same way, causing them to develop identical errors.
- Crosstalk: unintended interactions between qubits can introduce noise into the system.
- Accumulating error rates: as more quantum gates are applied, the probability of multiple qubits being affected by errors increases exponentially.
This means that a quantum computer with just Shor’s code is not reliable enough for practical applications.
Error Detection Itself Can Fail
Quantum error correction is not just about correcting errors—it also involves detecting them without disturbing the quantum state.
However, real quantum hardware introduces measurement errors, meaning that even the error detection process is not perfect. If we misidentify an error, we might apply the wrong correction, making things worse.
Logical Qubits Require Continuous Error Correction
Even if we successfully correct errors once, quantum state remain fragile. Decoherence constantly affects qubits, requiring continuous error correction throughout a computation.
For a logical qubit to be truly useful, it must be able to:
- Detect and correct errors repeatedly before decoherence destroys the quantum state
- Operate under high-fidelity measurements to ensure accurate error detection
- Support real-time feedback loops to apply corrections as soon as errors appear
Shor’s 9-qubit code does not provide continuous fault tolerance, meaning it cannot maintain a logical qubit indefinitely.
The leading error correction approach for practical fault-tolerant quantum computing is the surface code, which requires hundreds to thousands of physical qubits per logical qubit—far more than Shor’s 9-qubit code.
Currently, the world’s most advanced quantum computers still struggle to create large-scale, reliable logical qubits. As of 2025, the highest world record for logical qubit is just 24 qubits (source).
All images were drawn by the author—except the first, generated by ChatGPT.

Leave a comment