Deutsch-Jozsa Algorithm: a Simple Quantum Supremacy

An Introduction to the Quantum Supremacy

The Deutsch-Jozsa algorithm is one of the first quantum algorithms that showed a significant speedup over its classical counterpart. Proposed by David Deutsch and Richard Jozsa in 1992, this algorithm serves as a stepping stone for understanding the potential of quantum computing.

While advanced algorithms like Shor’s algorithm (which can factorize large numbers in polynomial time) illustrate the power of quantum computation, they can be overwhelming for beginners. In contrast, the Deutsch-Jozsa algorithm is conceptually simpler and is often used as an introductory example to showcase the advantages of quantum computing. In this article, we’ll explore the Deutsch-Jozsa algorithm in detail.

Problem Statement

The Deutsch-Jozsa problem is a simple decision problem that can be solved efficiently using a quantum computer. The problem is defined as follows:

Given a function $f: \braces{0, 1}^n \to \braces{0, 1}$, where $n$ is the number of bits in the input, determine whether the function is constant or balanced.

• A function is constant if it returns the same value (either $0$ or $1$) for all possible inputs.
• A function is balanced if it returns $0$ for exactly half of the inputs and $1$ for the other half.

Classical Solution

In the classical approach, determining whether $f$ is constant or balanced requires evaluating $f$ for multiple inputs. In the worst-case scenario, we need to check at least $2^{n-1} + 1$ inputs. This is because even if the first half of the inputs return the same value (e.g., all $0$ or $1$), we cannot be certain whether $f$ is constant or balanced without evaluating additional inputs.

This exponential growth in the number of function evaluations highlights the inefficiency of the classical approach for large $n$.

Quantum Solution: Deutsch-Jozsa Algorithm

The Deutsch-Jozsa algorithm solves this problem using just a single(!!) query to the function $f$, which is exponentially faster than the classical method.

Overall Structure

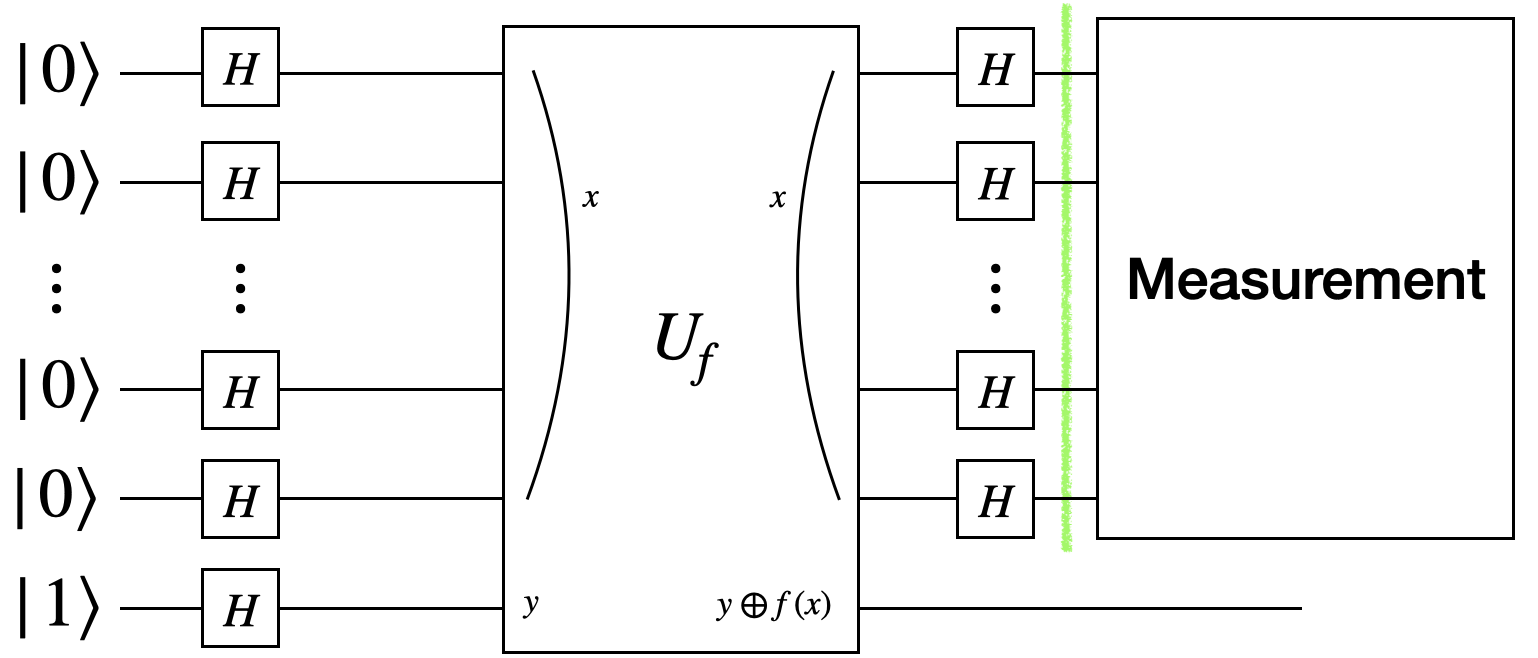
The Deutsch-Jozsa algorithm is implemented as a quantum circuit, shown below:

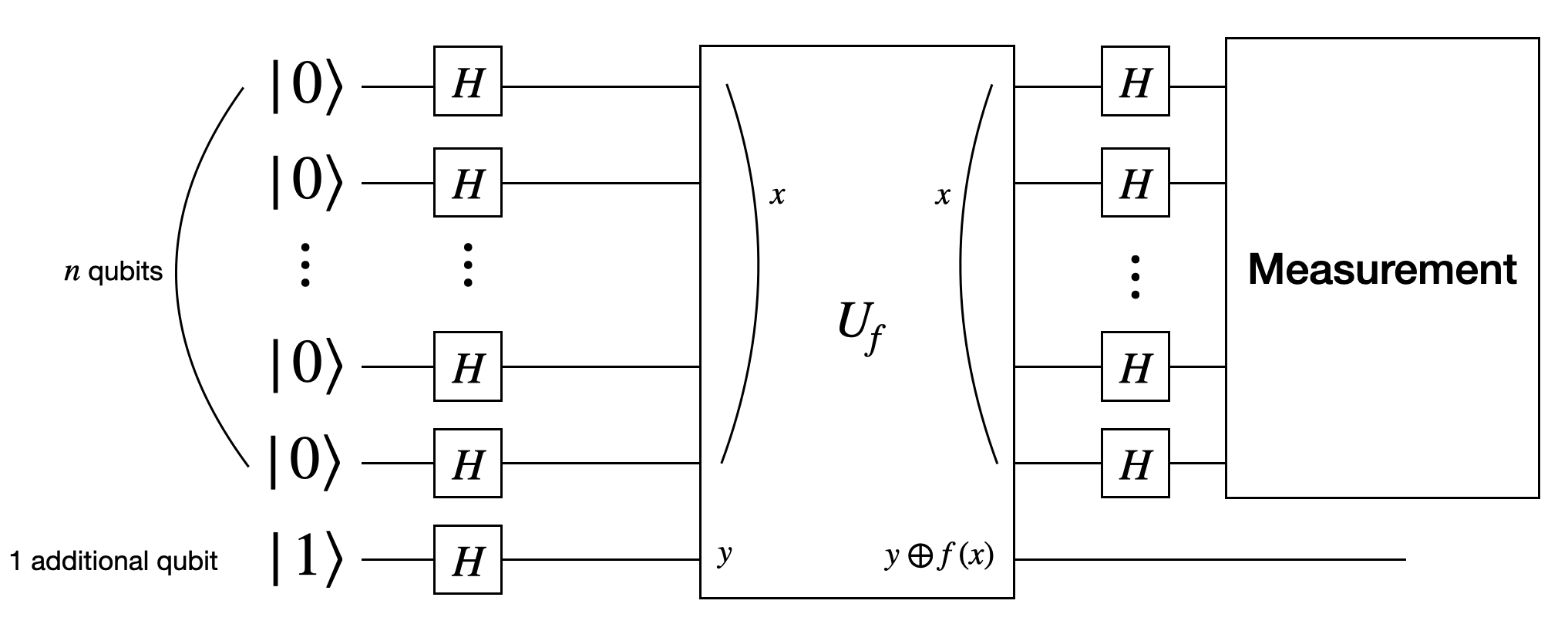
Most components of this circuit should be familiar by now, except for $U_f$, the quantum version of the function $f$. The $U_f$ gate is a multi-qubit unitary gate that implements the behavior of $f$. It is a black-box operation, meaning we can query it but do not know its internal details of its implementation.

Here’s how $U_f$ works:

• The first $n$ qubits are the input qubits, representing the input $x\in\braces{0, 1}^n$.
• The last qubit is the output qubit, whose state is manipluated by $U_f$.

The action of $U_f$ is defined as:

\[U_f\prths{\ket{x}\otimes\ket{y}} = \ket{x}\otimes\prths{\ket{y\oplus f(x)}},\]

where $\oplus$ denotes the bitwise XOR operation. The output qubit($y$) is flipped based on the value of $f(x)$.

Key Components of the Circuit

• Qubits: $n+1$ qubits, where $n$ is the number of input bits.
• Gates:
  • Hadamard gate $H$: applied to all qubits at the beginning of the circuit.
  • $U_f$: queries the function $f$.
  • Another set of Hadamard gates $H$: applied to the input qubits only after querying $U_f$.
• Measurement: performed on the input qubits at the end of the circuit to determine whether the function $f$ is constant or balanced.

Let’s now break down the steps of the algorithm in detail.

Step-by-Step Explanation

We will follow the circuit step by step, moving from left to right, to understand how the Deutsch-Jozsa algorithm works. The green vertical line in the diagrams indicates the current step in the circuit.

1. Initialization

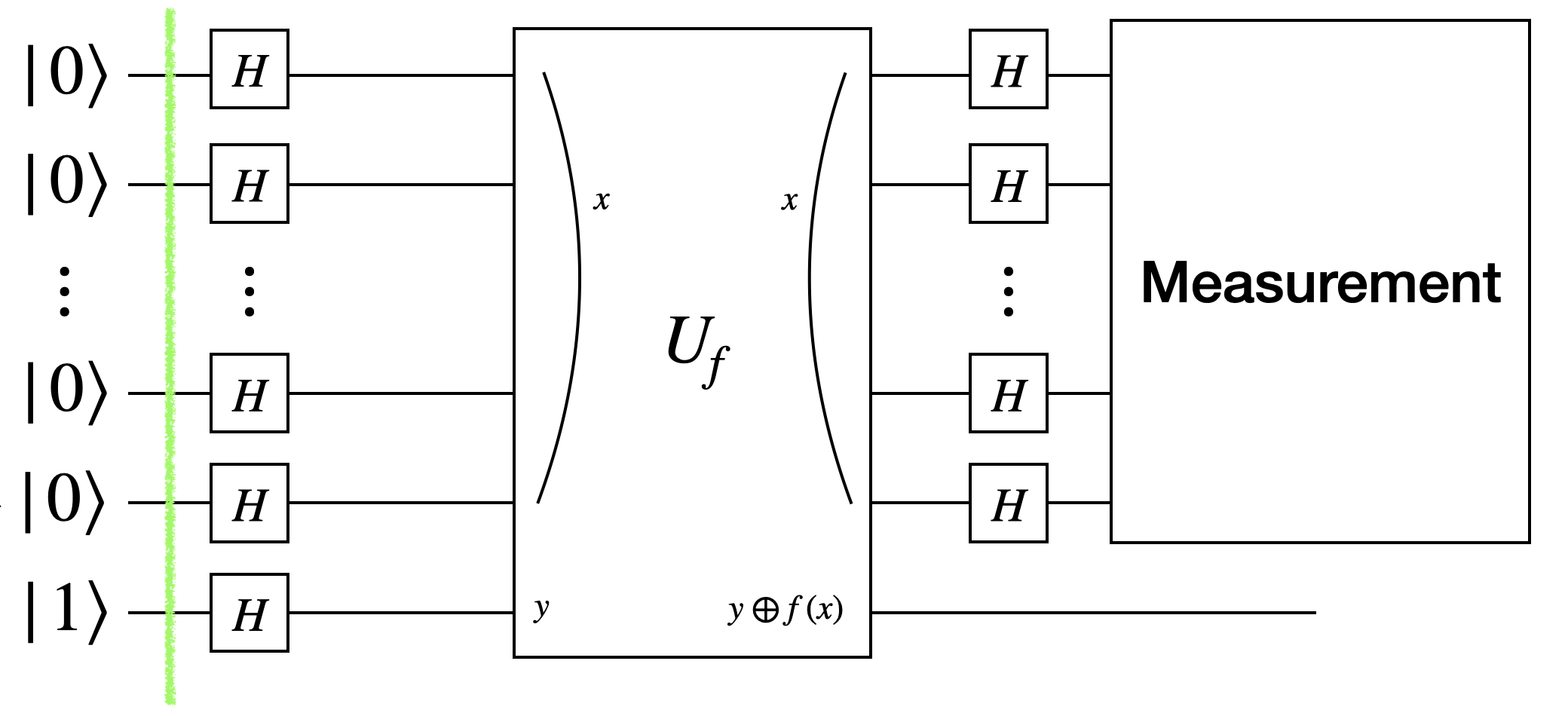
The algorithm begins by initializing the $n+1$ qubits as follows:

• Input qubits: $\ket{0}^{\otimes n}=\ket{0}\otimes\ket{0}\otimes\ldots\otimes\ket{0}$
• Output qubit: $\ket{1}$

Thus, the combined state of all $n+1$ qubits is:

\[\ket{\psi_1} = \ket{0}^{\otimes n}\otimes\ket{1}.\]

2. Applying Hadamard Gates

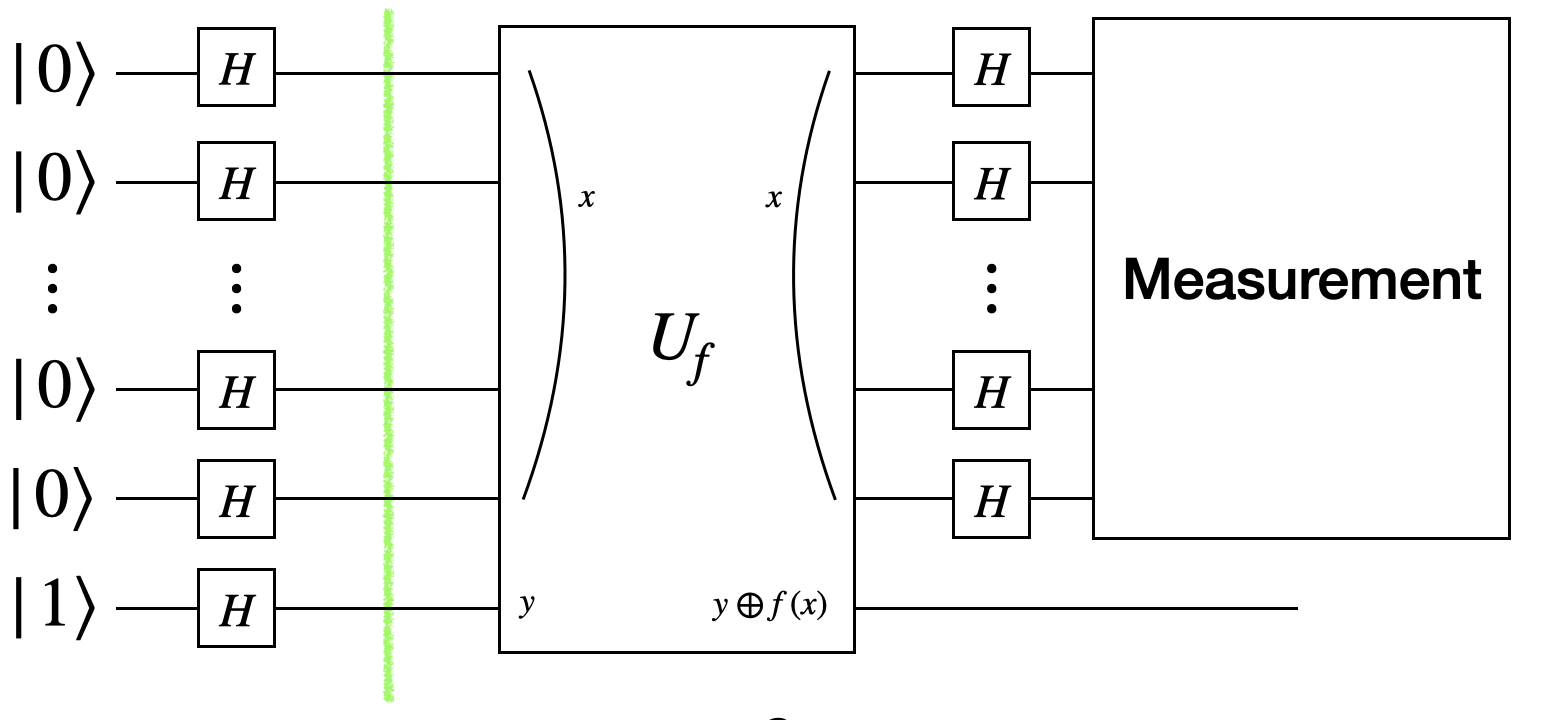
Next, a Hadamard gate $H$ is applied to all $n+1$ qubits. The Hadamard gate creates superposition, transforming the qubits as follows:

\[\begin{align*} \ket{\psi_2} &= \prths{H\ket{0}}^{\otimes n}\otimes\prths{H\ket{1}} \\ &= \prths{\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})}^{\otimes n}\otimes \prths{\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})} \\ &= \frac{1}{\sqrt{2^n}}\prths{\ket{00\ldots0}+\ket{00\ldots1}+\ldots+\ket{11\ldots1}} \otimes\frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}\ket{x} \otimes\frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}}. \end{align*}\]

Note that, the input qubits (first $n$) are now in a superposition of all possible $n$-bit binary strings $\ket{x}$, while the output qubit is in the state $\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$.

3. Querying the Function $U_f$

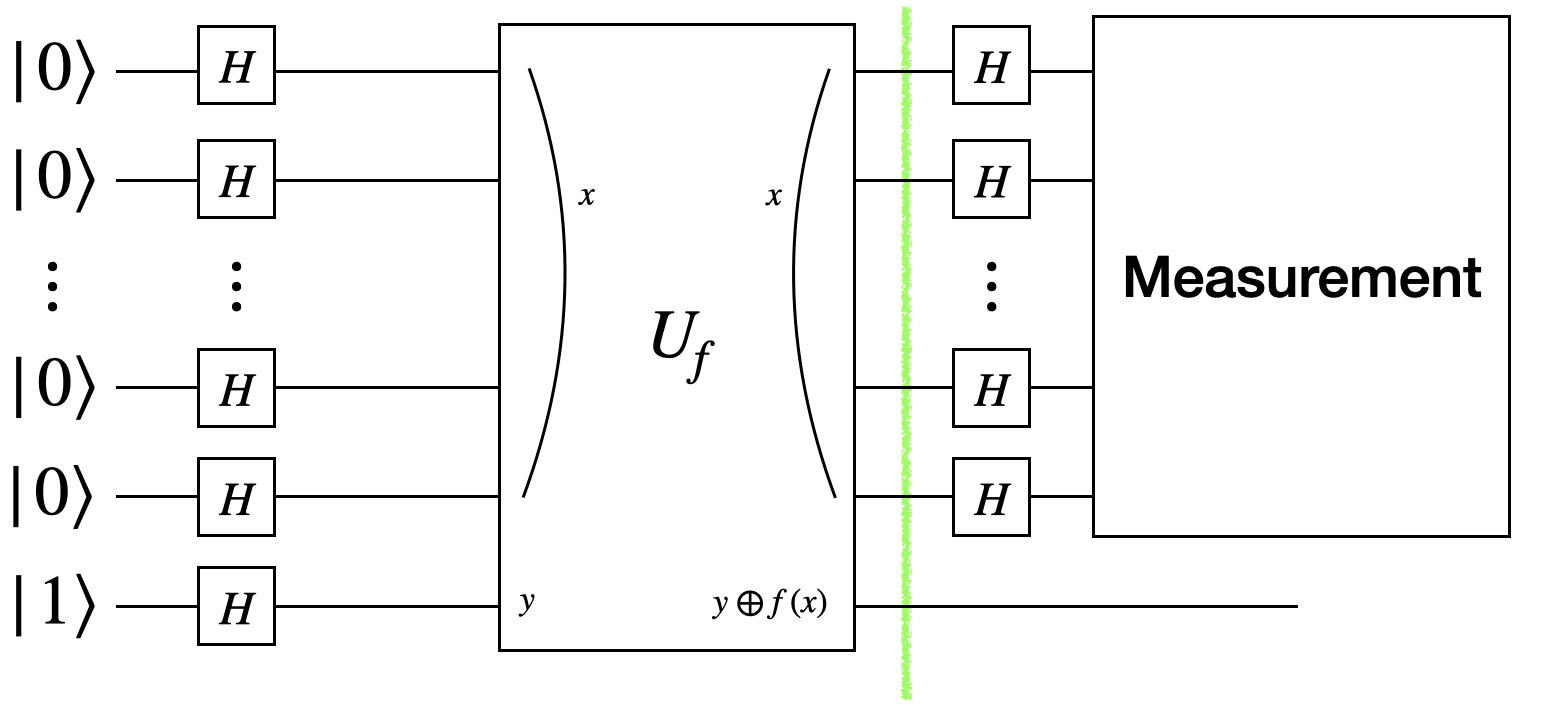
Next, the unitary oeprator $U_f$ is applied, encoding the function $f(x)$. The action of $U_f$ on the state $\ket{\psi_2}$ is:

\[\begin{align*} \ket{\psi_3} &= U_f\ket{\psi_2} \\ &= U_f\prths{\frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}\ket{x} \otimes\frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}}} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}U_f\prths{\ket{x} \otimes\frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}}} \end{align*}\]

The first $n$ qubits represent the input $x$, and the last qubit is the output qubit. $U_f$ flips the state of the output qubit based on $f(x)$. Since the output qubit starts in the superposition state $\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$, the action of $U_f$ on the system becomes:

\[\ket{\psi_3} = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}\ket{x}\otimes \frac{1}{\sqrt{2}}\prths{\ket{f(x)}-\ket{1\oplus f(x)}}.\]

For $f(x)\in\braces{0, 1}$, $\ket{f(x)}-\ket{1\oplus f(x)}$ can be written as

• If $f(x)=0$, $\ket{0}-\ket{1}$.
• If $f(x)=1$, $\ket{1}-\ket{0}$.

Thus, $\ket{f(x)}-\ket{1\oplus f(x)}$ simplifies to $(-1)^{f(x)}(\ket{0}-\ket{1})$. Substituting this back into the equation, we get:

\[\ket{\psi_3} = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}\ket{x}\otimes \frac{1}{\sqrt{2}}\prths{\ket{0}-\ket{1}}.\]

Now, the output qubit no longer plays a role in the computation, so we focus only on the state of the input qubits. This reduced state is:

\[\ket{\psi_3^\prime} = \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}\ket{x}.\]

This state encodes the function $f(x)$ in the relative phase(sign) of the input qubits.

4. Applying Hadamard Gates to Input Qubits

The fourth step applies the Hadamard gate $H$ to the input qubits only. This transforms the input qubits’ state as follows:

\[\begin{align*} \ket{\psi_4} &= H^{\otimes n}\ket{\psi_3^\prime} \\ &= H^{\otimes n}\prths{\frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}\ket{x}} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}H^{\otimes n}\ket{x} \end{align*}\]

What should we do with $H^{\otimes n}\ket{x}$? We can expand it as:

\[\begin{align*} H^{\otimes n}\ket{x} &= H^{\otimes n}\prths{\ket{x_1}\otimes\ket{x_2}\otimes\ldots\otimes\ket{x_n}} \\ &= H\ket{x_1}\otimes H\ket{x_2}\otimes\ldots\otimes H\ket{x_n} \\ &= \prths{\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_1}\ket{1})}\otimes \prths{\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_2}\ket{1})}\otimes\ldots\otimes \prths{\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_n}\ket{1})} \\ &= \frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1}(-1)^{x\cdot y}\ket{y}, \end{align*}\]

where $x\cdot y$ denotes the bitwise inner product of $x$ and $y$. For example, if $x=101$ and $y=110$, then $x\cdot y=1\cdot1+0\cdot1+1\cdot0=1$.

It’s a bit tricky to understand the expansion, but it’s simply a polynomial expansion. Each possible $n$-bit binary string $y$ contributes a term in the sum, with a phase factor $(-1)^{x\cdot y}$ determined by the bitwise inner product.

To clarify further, let’s expand $H^{\otimes 2}\ket{10}$ as an example:

\[\begin{align*} H^{\otimes 2}\ket{10} &= H^{\otimes 2}\prths{\ket{1}\otimes\ket{0}} \\ &= H\ket{1}\otimes H\ket{0} \\ &= \prths{\frac{1}{\sqrt{2}}(\ket{0}+(-1)^1\ket{1})}\otimes \prths{\frac{1}{\sqrt{2}}(\ket{0}+(-1)^0\ket{1})} \\ &= \frac{1}{\sqrt{2}}\prths{\ket{00}+\ket{01}-\ket{10}-\ket{11}}. \end{align*}\]

If the expansion still seems confusing, it’s fine to trust the result and move on. The key takeaway is the transformation:

\[H^{\otimes n}\ket{x} = \frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1}(-1)^{x\cdot y}\ket{y},\]

which shows the Hadamard gate create a superposition with phase factors determined by the bitwise inner product $x\cdot y$.

Using this fact, we can now rewrite $\ket{\psi_4}$ as:

\[\begin{align*} \ket{\psi_4} &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}H^{\otimes n}\ket{x} \\ &= \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}\prths{\frac{1}{\sqrt{2^n}}\sum_{y=0}^{2^n-1}(-1)^{x\cdot y}\ket{y}} \\ &= \frac{1}{2^n}\sum_{x=0}^{2^n-1}\sum_{y=0}^{2^n-1}(-1)^{f(x)}(-1)^{x\cdot y}\ket{y} \\ &= \sum_{y=0}^{2^n-1}\prths{\sum_{x=0}^{2^n-1}\frac{1}{2^n}(-1)^{f(x)+x\cdot y}\ket{y}}. \end{align*}\]

Now, the coefficients of each $\ket{y}$ encode the behavior of the function $f(x)$. The remaining step will reveal whether $f(x)$ is constant or balanced on these coefficients.

5. Measurement

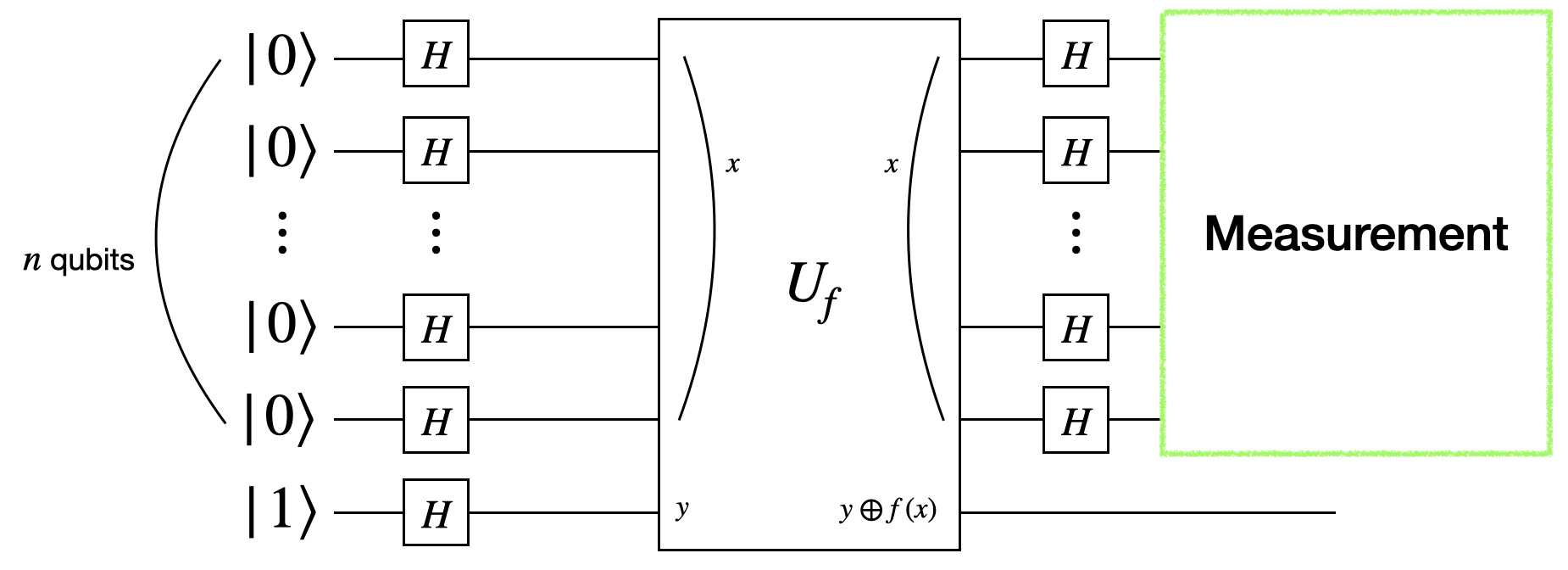
The final step is to measure the state $\ket{\psi_4}$. The probability of $\ket{\psi_4}$ collapsing into a specific computational basis state, such as $\ket{0\ldots0}$, $\ket{0\ldots1}$, $\ldots$, $\ket{1\ldots1}$, depends on the absolute square of the coefficients associated with these states.

Let’s analyze the probability of measuring the state $\ket{0\ldots0}$. The coefficient of $\ket{0\ldots0}$ in the sum for $\ket{\psi_4}$ is given by:

\[\sum_{x=0}^{2^n-1}\frac{1}{2^n}(-1)^{f(x)+x\cdot0\ldots0}.\]

Since $x\cdot0\ldots0=0$ (the bitwise inner product with the all-zero vector is always zero), this simplifies to:

\[\sum_{x=0}^{2^n-1}\frac{1}{2^n}(-1)^{f(x)} = \frac{1}{2^n}\sum_{x=0}^{2^n-1}(-1)^{f(x)}.\]

Evaluating the Sum

• If $f(x)$ is constant, all terms in the sum $(-1)^{f(x)}$ are the same:

  • If $f(x)=0$, then $(-1)^{f(x)}=1$ for all $x$, and the sum is:

    \[\sum_{x=0}^{2^n-1}1 = 2^n.\]

  • If $f(x)=1$, then $(-1)^{f(x)}=-1$ for all $x$, and the sum is:

    \[\sum_{x=0}^{2^n-1}(-1) = -2^n.\]

    The sum is $\pm 2^n$, so the coefficient of $\ket{0\ldots0}$ is $\pm 1$. The probability of measuring $\ket{0\ldots0}$ is:

    \[\prths{\pm 1}^2=1.\]

• If $f(x)$ is balanced, half of the terms in the sum $(-1)^{f(x)}$ are $1$ and the other half are $-1$. Therefore, the sum cancels out to $0$, and the coefficient of $\ket{0\ldots0}$ is $0$:

  \[\sum_{x=0}^{2^n-1}(-1)^{f(x)} = 0.\]

  The sum is $0$, so the coefficient of $\ket{0\ldots0}$ is $0$. The probability of measuring $\ket{0\ldots0}$ is:

  \[0^2=0.\]

Conclusion

• If the measurement result is $\ket{0\ldots0}$, then $f(x)$ is constant.
• If the measurement result is any other state, then $f(x)$ is balanced.

This completes the Deutsch-Jozsa algorithm. By querying the function $f$ just once, we can determine whether $f$ is constant or balanced with certainty.